こんにちは。札幌自学塾・新道東店の講師、五十嵐です。
3回目となる合同証明の記述問題、今回からちょっとだけ難易度が上がります。
前回の記事や塾長のYouTube動画講座も併せてご覧ください。
※前回記事で取り上げた問題、実は、今回リンクを貼っている塾長の動画の問題と同じです。
合同証明の記述問題~その3~


問3.
次の図で、△ABC、△CDEは正三角形である。このとき、△ACD≡△BCE であることを証明しなさい。
・考え方
・解答例
考え方
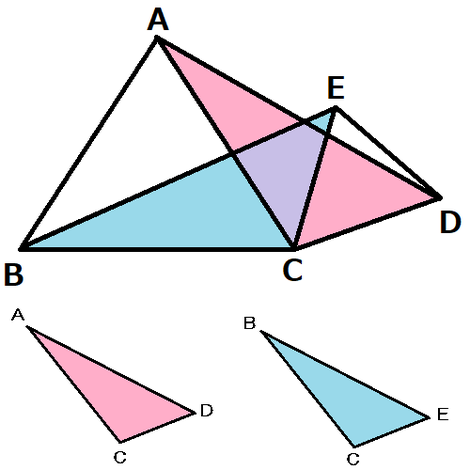
今回の問題は、前回と比べて設問文の文言がとてもシンプルです。
その代わり、図形が複雑に交わっているので、状況を正確に掴むことが求められます。
いつもどおり、まずは、ゴールを確認しましょう。
△ACD≡△BCE を証明することが目標です。
この2つの三角形が図中のどこを指しているのかを把握しましょう。
今回は、最初から2つの三角形を抜き出して解説します。

次に、設問文から読み取れる条件を図にどんどん書き入れてゆきたいです。
ところが、今回の問題は、今までの問題と違って「〇〇=□□」のように直接使える材料が明示されていません。
と言うよりも、明らかに「△ABC、△CDEは正三角形である。」という点から考えるしかないですよね。
「正三角形」という言葉から、全ての辺の長さが同じ(赤線・青線)で、全ての角の大きさが60°(緑)ということを導く必要があります。

これを今回の問題に当てはめると、AC=BC(赤)、CD=CE(青)、∠ECD=∠ACB=60°(緑)となります。
この図を見ると、あとは ∠ACD=∠BCE と言えれば「2組の辺とその間の角がそれぞれ等しい」と言うことができそうですね。
高校入試や定期試験では制限時間があるため、このように、予測をつけておくことも大切です。

今回の問題の山場です。
∠ACD(上の緑の部分)=∠ECD(●)+∠ACE(▲)
∠BCE(下の緑の部分)=∠ACB(●)+∠ACE(▲)

●は60°で同じ大きさの角、▲は共通の角なので、∠ACD=∠BCE(緑)となります。
言われてみれば簡単ですが、自分の力で気付くのはちょっと大変です。

以上で、AC=BC(赤)、CD=CE(青)、∠ACD=∠BCE(緑)と3つの材料が揃い、2組の辺とその間の角がそれぞれ等しいと言うことができるため、△ACD≡△BCE が成り立つと証明することができます。
解答例
△ACDと△BCEにおいて、
△ABC、△CDEは正三角形なので、
AC=BC・・・①、CD=CE・・・②、
∠ECD=∠ACB=60°・・・③
ここで、
∠ACD=∠ECD+∠ACE・・・④
∠BCE=∠ACB+∠ACE・・・⑤
よって、③、④、⑤より、∠ACD=∠BCE・・・⑥
①、②、⑥より、2組の辺とその間の角がそれぞれ等しいので、
△ACD≡△BCE
参考:ハイクラステスト数学(受験研究社)
