かんたん？むずかしい？合同証明の記述問題をマスターしよう！～その４～　栄南中・栄町中の生徒さんの挑戦を待っています！

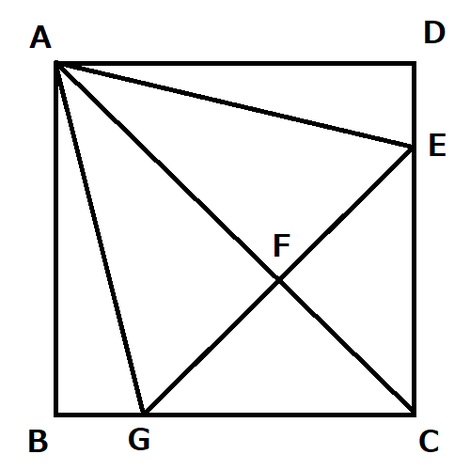
問４．

次の図のように、正方形ＡＢＣＤがある。辺ＣＤ上に、２点Ｃ、Ｄと異なる点Ｅをとり、点Ａと点Ｅを結ぶ。点Ｅから対角線ＡＣに垂線をひき、その交点をＦとする。また、２点Ｅ、Ｆを通る直線と辺ＢＣとの交点をＧとし、点Ａと点Ｇを結ぶ。このとき、△ＡＥＦ≡△ＡＧＦ であることを証明しなさい。

・考え方

・解答例

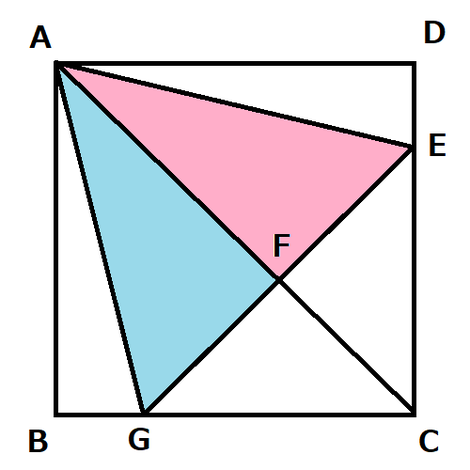
今回の考え方は、実際に私が問題を解くときの道筋をそのまま書いています。

最終的に少々トリッキーな解き方になるので、どのような順番で考えているのか、ぜひ注目してみてください。

いつもどおり、ゴールを確認するのは同じです。

△ＡＥＦ≡△ＡＧＦ を証明することが目標ですので、まずは、この２つの三角形が図中のどこを指しているのかを把握しましょう。

次に、設問文から読み取れる条件を図にどんどん書き入れてゆきます。

サクっと書くと、ＡＦは共通な辺（赤）、∠ＡＦＥ＝∠ＡＦＧ＝90°（青）です。

さて、あと１ヶ所の辺または角が等しいと言うことができれば無事に証明ができそう。

ここで、ちょっと踏み込んだ解説をします。

今回証明する合同な図形は、ただの三角形ではなく、直角三角形です。

そして、直角三角形の場合のみ使える合同条件として、次の２つがあります。

・斜辺と１つの鋭角がそれぞれ等しい

・斜辺と他の１辺がそれぞれ等しい

この合同条件を用いる場合のポイントとしては、必ず「斜辺が等しい」と示さなくてはなりません。

ですが、今回の問題では、斜辺に当たる ＡＥ＝ＡＧ（緑）を直接示すことができません。

そこで、通常の三角形の合同条件を考えてみます。

ＥＦ＝ＧＦ（図の左下・緑）と言うことができれば、２組の辺とその間の角がそれぞれ等しいと言えます。

∠ＥＡＦ＝∠ＧＡＦ（図の右下・緑）と言うことができれば、１組の辺とその両端の角がそれぞれ等しいと言えます。

さて、みなさんは ＥＦ＝ＧＦ または ∠ＥＡＦ＝∠ＧＡＦ と言うことができますか？

残念ながら、どちらも１手で直接示すことができません。手詰まりです。さぁ困りました。

今回の問題の最大の山場です。

この問題では、図を見ると分かるように、他にもいくつか三角形が登場しています。

その中で「この三角形だったら合同ってすぐ言えたんだけどなぁ…。」とガッカリするような図形がありませんか？

そう、△ＣＥＦと△ＣＧＦの組み合わせです。

そして、この三角形には、辺ＥＦと辺ＧＦが含まれています。

もし、△ＣＥＦ≡△ＣＧＦ と言うことができれば、合同な図形の対応する辺が等しいことから、ＥＦ＝ＧＦ が成り立ちます。

サクっと書くと、ＣＦは共通な辺（赤）、∠ＥＦＣ＝∠ＧＦＣ＝90°（青）、∠ＥＣＦ＝∠ＧＣＦ＝45°（緑）ですから、１組の辺とその両端の角がそれぞれ等しいので、△ＣＥＦ≡△ＣＧＦ となります。

そうすると、合同な図形の対応する辺は等しいので、ＥＦ＝ＧＦ（緑）となります。

△ＡＥＦと△ＡＧＦに戻って考えてみると、ＡＦは共通な辺（赤）、∠ＡＦＥ＝∠ＡＦＧ＝90°（青）、ＥＦ＝ＧＦ（緑）と３つの材料が揃い、２組の辺とその間の角がそれぞれ等しいと言うことができるため、△ＡＥＦ≡△ＡＧＦ が成り立つと証明することができます。

今回のように、合同な図形の対応する辺や角が等しいことを利用するケースもあります。

ある三角形の合同証明をするために、別の三角形の合同証明をする必要があるというのも面白いですね。