かんたん？むずかしい？合同証明の記述問題をマスターしよう！～その６～　栄南中・栄町中の生徒さんの挑戦を待っています！

 

問６．

次の図のような△ＡＢＣで、点Ｂと辺ＡＣの中点Ｍを結んだ直線と、点Ｃを通りＢＡに平行に引いた直線との交点をＤとする。このとき、四角形ＡＢＣＤが平行四辺形になることを証明しなさい。

 

・考え方

・解答例

・最後に

 

 

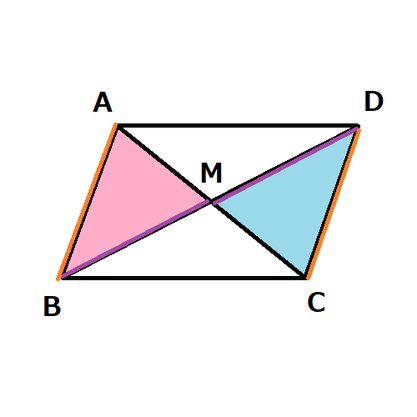
いつもどおり、設問文から読み取れる条件を図にどんどん書き入れてゆきます。

まずは「辺ＡＣの中点Ｍ」と書いてあることから、ＡＭ＝ＣＭ（赤）です。

 

 

さらに「点Ｃを通りＢＡに平行に引いた直線との交点をＤとする」と書いてあることから、ＢＡ//ＣＤ です。

平行線ときたら錯角を必ず確認！　∠ＢＡＭ＝∠ＤＣＭ（青●）、∠ＡＢＭ＝∠ＣＤＭ（青▲）です。

 

 

設問文の条件を一通り書き入れたので一度確認してみましょう。

なんとなく、△ＡＢＭと△ＣＤＭが合同になりそうな気がしませんか？

 

 

∠ＡＭＢ＝∠ＣＭＤ（緑）または ＡＢ＝ＣＤ（緑）と言えれば、１組の辺とその両端の角がそれぞれ等しいと言えるので、△ＡＢＭ≡△ＣＤＭ が成り立つと言えそうですね。

 

 

平行四辺形になることを証明するのに、三角形の合同が何の役に立つの？と思うかもしれません。

ですが、合同な図形の対応する辺が等しいことを利用することで、ＢＭ＝ＤＭ（紫）や、ＡＢ＝ＣＤ（橙）と言うことができます。

 

 

ここで、平行四辺形の条件を思い出してください。

前回の記事で一部に触れましたが、平行四辺形の５条件を覚えていない人もいるかもしれませんので、ちょっと確認してみましょう。

 

まずは、平行四辺形の定義です。

 

・２組の対辺がそれぞれ平行である

 

次に、平行四辺形の定理ですが、辺・角・対角線の３つに分けて着目します。

 

・２組の対辺がそれぞれ等しい

・２組の対角がそれぞれ等しい（図１）

・対角線がそれぞれの中点で交わる（図２）

 

最後に、上記の組合せで次のようになります。

 

・１組の対辺が平行でその長さが等しい（図３）

 

このような順番でおさえると、５条件を全て覚えやすいです。

前回の記事で触れていなかったものは図にしておきました。

 

 

話を戻すと、ＡＭ＝ＣＭ（赤）、ＢＭ＝ＤＭ（紫）であれば「対角線がそれぞれの中点で交わる」と言えます。

または、ＡＢ//ＣＤ、ＡＢ＝ＣＤ（橙）であれば「１組の対辺が平行でその長さが等しい」と言えます。

どうやら、ＢＭ＝ＤＭ（紫）や、ＡＢ＝ＣＤ（橙）と言うためにも、△ＡＢＭ≡△ＣＤＭ と言う必要がありそうですね。

 

 

では、改めて△ＡＢＭと△ＣＤＭの合同について考えてみると、対頂角が等しいので、∠ＡＭＢ＝∠ＣＭＤ（緑）と言えます。

 

これに、前述した ＡＭ＝ＣＭ（赤）、∠ＢＡＭ＝∠ＤＣＭ（青）を併せると、１組の辺とその両端の角がそれぞれ等しいと言えるので、△ＡＢＭ≡△ＣＤＭ が成り立ちます。

 

 

あとは、前述したように、合同な図形の対応する辺は等しいので、ＢＭ＝ＤＭ（紫）や、ＡＢ＝ＣＤ（橙）となります。

 

 

そして、ＡＭ＝ＣＭ（赤）、ＢＭ＝ＤＭ（紫）から「対角線がそれぞれの中点で交わる」と言えるため、四角形ＡＢＣＤが平行四辺形になると証明できます。

または、ＡＢ//ＣＤ、ＡＢ＝ＣＤ（橙）から「１組の対辺が平行でその長さが等しい」とも言えるため、四角形ＡＢＣＤが平行四辺形になると証明しても構いません。