こんにちは。札幌自学塾・新道東店の講師、五十嵐です。
5回目となる合同証明の記述問題、今回は、今年の入試で最も出題される可能性が高い(私の勝手な想像です)問題です。
前回の記事や塾長のYouTube動画講座も併せてご覧ください。
合同証明の記述問題~その5~


問5.
次の図のように、平行四辺形ABCDの対角線AC上に ∠ABE=∠CDF となるように、点E、Fをとる。このとき、△ABE≡△CDF となることを証明しなさい。
・五十嵐先生の出題予想!?
・考え方
・解答例
五十嵐先生の出題予想!?
冒頭で「今年の入試で最も出題される可能性が高い」と私が予想した理由は「平行四辺形の性質を利用した問題」であるからです。
これまでの私の記事では、正方形や正三角形の性質を利用した証明問題を掲載してきましたが、平行四辺形の性質はその数が多く、より狙われやすいと考えています。
そのため、平行四辺形の性質を利用した三角形の合同証明や、次回記事で取り上げる平行四辺形の証明が出題されるのではないかと予想しています。
(あくまでも予想です。根拠はありません。でも公立入試で本当に出題されたら褒めてください。)
考え方

まずは、ゴールを確認します。
△ABE≡△CDF を証明することが目標です。
まずは、この2つの三角形が図中のどこを指しているのかを把握しましょう。

次に、設問文から読み取れる条件を図にどんどん書き入れてゆきます。
簡単なところでは、仮定より、∠ABE=∠CDF(赤)です。
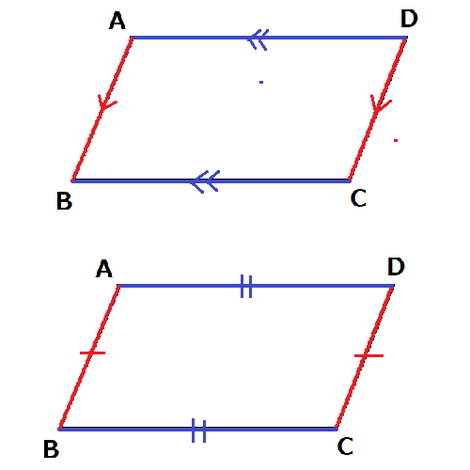
設問文に書かれている残りの条件は、四角形ABCDが平行四辺形であることくらいです。
ここで、平行四辺形の性質について考えてみましょう。
平行四辺形の性質はかなり多くありますが、今回用いるのは次の2つです。
・対辺が平行である(AB//DC、AD//BC)
・対辺の長さが等しい(AB=DC、AD=BC)

この性質を用いると、まずは、平行四辺形の対辺が等しいので、AB=CD(青)と言えます。

さらに、平行四辺形の対辺が平行であることから、錯角が等しいと言えますので、∠BAE=∠DCF(緑)が成り立ちます。
平行線といえば錯角です!絶対に見逃さないでください!

以上で、∠ABE=∠CDF(赤)、AB=CD(青)、∠BAE=∠DCF(緑)と3つの材料が揃い、1組の辺とその両端の角がそれぞれ等しいと言えるので、△ABE≡△CDF が成り立つと証明できます。
ちなみに、今回取り上げた問題はかなり簡単な方ですが、平行四辺形の性質を理解していないと正答できませんので、わからなかった人はしっかりと復習しておいてください。
解答例
△ABEと△CDFにおいて、
仮定より、∠ABE=∠CDF・・・①
平行四辺形の対辺は等しいので、AB=CD・・・②
平行四辺形の対辺は平行で、錯角が等しいので、∠BAE=∠DCF・・・③
①、②、③より、1組の辺とその両端の角がそれぞれ等しいので、
△ABE≡△CDF
